We continue from Part 49.
Let us recall the notation used there: H is a separable Hilbert space, with the scalar product (x,y), A = B(H) is the von Neumann algebra of all bounded operators on H, ρ is a (faithful) density matrix in the ideal of trace-class operators, B2(H) is the ideal of Hilbert-Schmidt operators with the scalar product <X,Y> = Tr(X*Y), we have B1(H)⊂B2(H)⊂B(H), en (n=1,2,....) is an orthonormal basis consisting of eigenvectors of ρ in H, so that
ρ = ∑n pn Pn, pn>0, ∑n pn = 1,
where Pn are orthogonal projections on en.
Notice that if H is infinite-dimensional, then limn pn = 0 (Why?), so that, in this case 0 is an accumulation point in the spectrum of ρ.
It is useful to have an orthonormal basis in the Hilbert algebra B2(H). To this end we define em,n∈B2(H)
em,n ≐ |em)(en|
where
|em)(en| x = (en,x)em.
Exercise 1. Prove that em,n∈B2(H).
Then they indeed form an orthonormal basis in B2(H).
Exercise 2. Prove the last statement. Hint: to show that we have a basis consider the space of all finite linear combinations of Emn.
Use the fact that a subspace is dense in a Hilbert space if and only if
the only vector orthogonal to all vectors of the subspace is the zero
vector.
Exercise 3☺. Show that, with the notation as above, Pn = em,n.
In the following we shall employ a convenient notation used by Connes and Rovelli in their paper [1]. Given an element a∈A, it can be considered as a bounded operator in B(H). But if it is a Hilbert-Schmidt operator, it is an element of the Hilbert space B2(H). In the later case we will write it as | a >. Thus, for example,
Ωρ = | ρ½ >. (1)
The representations π and π' of A on B2(H) become resp.
π(a)| b > = | ab >, π'(a)| b > = | ba >.
For the scalar product we can write
<a,b> = < a | b > = Tr(a*b).
The Tomita-Takesaki construction provides us with two (super-) operators: the anti-unitary involution J, and the unitary "Tomita flow" s ⟼ Uρ(s), s ∈ R.
The involution J
We consider first the anti-unitary (super-) operator
J: B2(H) → B2(H),
defined by
J | a > = | a* >. (2)
We immediately get the anti-unitary property (How?):
<JS , JT> = cc(<T , S>), S,T in B2(H),
where cc stands for the complex conjugate.
We also have J2 = 1 (the identity operator). Moreover, we have
JΩρ = Ωρ , for any density matrix ρ.
Notice that, in our context, J does not depend on ρ - it is "universal".
We have
Jπ(A)J = π'(A).
Indeed, for any a∈A, b∈B2(H), we have
Jπ(a)J| b > = Jπ(a)| b* > = J| ab* > = | ba*> = π'(a*) | b >.
Therefore Jπ(a)J = π'(a*), and the equality Jπ(A)J = π'(A) follows (Why?). But π'(A) = π(A)', therefore J transforms the von Neumann algebra π(A) into its commutant, and vice versa (as it follows from J2=1).
Tomita's thermal flow
Tomita's flow Uρ(s) is defined by the formula:
Uρ(s)| a > = | ρisaρ-is >, a∈B2(H), s∈R. (3)
The formula above requires an explanation. Here it comes. First of all what is ρis? Here we use Fig. 1 of Part 49, with integrals replaced by infinite sums. Since
ρ
= Σn pn Pn, is a spectral resolution of ρ, ρis is defined as:
ρis = ∑n pnis Pn.
But what is λis (here for λ>0)? It can be defined as
λis = eis log λ,
where log stands for the natural logarithm.
For λ>0 and s real, it is a complex number of modulus 1, thus nothing special. We thus have
ρis = ∑n eis log pn Pn. (4)
It follows then from the last statement in Fig 1 that ρis is a unitary operator in B(H) (How?). Moreover, denoting
Uρ(s) = ρis = eis log(ρ), (5)
we have (How?)
Uρ(s) Uρ(s') = Uρ(s+s'),
so that we have a one-parameter group of unitary operators on H. Denoting
αs(a) = Uρ(s) a Uρ(s)*, a∈A,
we have a one-parameter group of *-automorphisms of A. It is called the group of modular automorphisms. It is this group that is called the Tomita modular flow. We notice that (Why?)
Uρ(s) Ωρ = Ωρ,
so that the vector Ωρ, representing the state, is invariant under Uρ(s). We can also write it as the invariance of the state ω under the modular flow
ω(αs(a)) = ω(a), s∈R.
References
[1] A. Connes, C. Rovelli, "Von
Neumann algebra automorphisms and time-thermodynamics relation in generally covariant quantum theories",
Class. Quantum Grav. 11 (1994) 2899 .
To be continued ....
P.S. 17-03-25 7:16 Changed the notation in the original post. Replaced Pm,n by em,n. Pm,n was suggestive of "Projectors". But these are basis vectors of B2(H), and not projectors. Notice that em,n* = en,m.Ifis a subset of an algebra
, we define its commutant
to be the set of all elements of
that commute with all the elements of
.
Observe thatis a subalgebra of
(straightforward).
The double commutantof
is
.
Similarly,.
Alwaysand
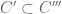
(let. If
then
. That is
'.
Now letso that for all
, we have
.
Now for any,
so
commutes with everything in
.
That is.
The text claims that in fact.
Now let. Now
, for all
.
Howeverso therefore
for all
.
That isalso.).
Ifis a normed algebra, then
is closed (with more structure we could show this as follows.
Defineby
. Now
is closed as is
.).
Ifis a *-algebra and
is self-adjoint, then
is a *-subalgebra of
(straightforward).







Something seems to be eaten in Eq. (5).
ReplyDeleteIt was an overdose of equalities. Thanks.
DeleteThis nice post brought from memory one of my favorites during college days, statistical mechanics course and famous Boltzmann formula, S=k*ln(W). So now I have a desire and "need" to actually refresh my memory with those generator functions and three kinds of ensembles we talked about, if memory still serves me well.
ReplyDeleteBut, before going down that lane, I owe you a geometric, or as close to possible to a geometric explanation of a spinor. So, here's the current understanding of that concept in geometrical terms.
Take a normal to a plane, or any vector representing a direction orthogonal to some plane, rotate it in any plane, which would be perpendicular to the plane of origin, while simultaneously rotating the original plane.
To get back in the same position it would take a 2pi rotation in the plane where the normal actually rotated, and a 2pi rotation of the plane of origin that the normal stands for. After half of a full rotation of the normal vector and the plane it stands for, the vector would be pointing in the opposite to its starting original direction, i.e. a "coupled" rotation for in total 2pi gives spatial reflection, which would explain so called two valuedness of a spinor.
In terms of geometrical bodies, this can be represented by a coupled orthogonal rotations of a simple ball, one as angle phi and the other as angle theta in spherical coordinates, or in terms of geography, along the longitudinal and latitudinal lines or directions.
Would that be satisfactory enough for your taste?
"In terms of geometrical bodies, this can be represented by a coupled orthogonal rotations of a simple ball, one as angle phi and the other as angle theta in spherical coordinates, or in terms of geography, along the longitudinal and latitudinal lines or directions."
DeleteMoreover, by rotating the torus on the sphere, we obtain the group SU(2).
P.S. After thinking a bit more about the spinor geometrical representation, any two coupled rotations of a ball or a sphere around non-collinear axes would most probably do the job, while the spatial reflection would be defined in relation to the other rotation, not of the spinor itself, but of the plane that rotates together with it.
DeleteKind of like the rotation of planet Earth while following or going along the lines of geomagnetic field. The opposite of the North geomagnetic pole is the South geomagnetic pole, that's its rotation for angle pi, while Earth's equatorial plane at the same time rotates it for additional angle pi, which makes it reflected over that plane.
So the 2pi rotation in any case other than two exactly perpendicular rotations, or around collinear axes, gives only the projection onto the axis of the plane's rotation in the opposite direction, while the actual pointing direction of a spinor remains on the same side, so to say.
In terms of longitude and latitude, the rotation for 2pi would put us just on the opposite parallel, while "keeping" us on the same meridian at the end, where we were when we started the rotation.
Sort of in contrast to the title of the Holmes' book Ark shared with us in part 45. :)
Well, not exactly in contrast to the book title, as in half a day the meridian where we started our journey would be on the other side of the Earth in relation to for example it's orbital velocity or momentum, which seems to not exactly solve the issue, as for 2pi rotation spinor object switches the sign of its projection to momentum direction, if understand correctly what SU(2) stands for.
DeleteAs a matter of fact, encountered just the similar kind of thing while playing with qq*. To have the product of two real biquaternions, let's say nabla_4' and qq*, to be real valued, easiest way to square that was to choose two different values of free parameter φ3, for e1 φ3=-pi/2, while for e2 φ3=-pi.
In relation of our spinor's geometrical representation here, it can perhaps be translated as reflection and rotation, done sort of independently, at the same time. In short, while being reflected over the equatorial plane, represented by angle pi, the plane also rotates for pi, making us find ourselves on the other side, on the same meridian even half a day later.
FWIW.
And this let's say coupled reflection+rotation then also explains why we have Pauli's exclusion principle for fermions, i.e. due to reflection over let's say the plane of rotation, along let's say shortest distance to the plane or along the same meridian, we can only have two essentially different states, latitude North and latitude South on that same meridian.
DeleteExcept in two cases, when being on the poles or on the axis of rotation, when reflection moves us to the opposite pole, situation that probably can represent vector bosons like photons, and when being on equator, when there is no reflection at all, which probably could represent scalar spin=0 types, which can be geometrically represented by simple rotating balls or spheres.
FWIW.
"And this let's say coupled reflection+rotation then also explains why we have Pauli's exclusion principle for fermions, i.e. due to reflection over let's say the plane of rotation, along let's say shortest distance to the plane or along the same meridian, we can only have two essentially different states, latitude North and latitude South on that same meridian."
DeleteMaybe more in the spirit of the "Meeting at a Far Meridian" book title, and perhaps better said, while a fermion oscillates or vibrates along his chosen meridian, only way to have a balanced system of two of them oscillating with the same frequency would be to have the other on the opposite or far meridian, while the whole system spins or rotates, maybe (probably) with the same frequency, which then can perhaps be seen as particle-wave duality.
In that sense, photons, with their oscillations, in like perfect counter phases, along the whole of the sphere's meridians, would be effectively rotating at the same time about two perpendicular axes. Infinite number of possibilities to choose those two axes through a sphere for a given rotation frequency, i.e. energy, would enable so called boson condensation.
Particle-antiparticle creation of light would then happen when two "identical" fermions oscillate each on its respective counter-meridian in counter phase, making perfectly balanced system (not that antiparticles would be some kind of holes). That would in a sense make electric charge sort of mode of vibration or of harmonic oscillator, similar to how photon energy are represented by quanta, which mathematically could be represented as oscillating in opposite time directions.
Does what's described make reasonable sense to others here?
In other words, in short, original rotation would represent energy as mass, which would essentially have no let's say counter phase to itself, thus leading to no negative energy or negative mass particles.
DeleteOscillations or vibrations corresponding to the original rotation frequency would represent electric charge, but not as separate let's say observable from mass, but as q/m, as there are no known charged particles that are massless, at least I haven't heard of any.
Possibility to have vibrations in counter phases results in let's say two possible charge orientations.
Tentatively, in that sense, originally initial charged particle would be electron, while proton as such would be sort of composite, but not of quarks as charged particles with thirds of electron electric charge, but of probably three coupled electron type charged particles.
The details need a bit of work out still, or as Ark would say, the devil is in the details.
Yeah, neutrinos, they probably hardly even make complete that original rotation, preceding any discussion about being electrically charged, which makes them still fermions as they would effectively still oscillate or vibrate, in effort to finally succeed in completing the full round of rotation, hence their minimal mass as the C's suggested when asked about neutrinos.
Delete@Saša, maybe you will find something useful here for your geo-physical analogies
Deletehttps://www.researchgate.net/publication/325226826_Chaotic_dynamics_of_an_electron
Thank you Igor.
Delete@Saša, "Sort of in contrast to the title of the Holmes' book Ark shared with us in part 45"
DeleteThank you for 'double-rotation' interpretation of spinors, it seems to be rather illustrative. I would say it is a continuation and generalization of the Efremov 'two-gears' model (i've presented it somewhere earlier in the Blog).
"Yeah, neutrinos..."
Delete@Saša, this reminds me of de Broglie's fusion theory, according to which fermions of spin 1/2 are fundamental, and bosons are their (fermion) tensor products of even degree. Thus, according to de Broglie, even light (photon) is a combination of two neutrinos. This is the famous (and forgotten) neutrino theory of light by de Broglie, which no one has ever been able to refute (in this statement i rely on the knowledge of Vadim Varlamov).
Thanks Anna for your comments and references.
DeleteRegarding 2 neutrinos creating a photon, in the model described above it could not happen, as neutrinos would not be "complete" fermions with full rounded original mass state like electrons. FWIW.
"Thank you for 'double-rotation' interpretation of spinors, it seems to be rather illustrative. I would say it is a continuation and generalization of the Efremov 'two-gears' model (i've presented it somewhere earlier in the Blog)."
DeleteRemember Efremov's and Ark's multi-gear representation, but what I meant looks simpler than that, it's just that it seems my first presentation was of rather poor quality. And apologies for misquoting the "Meeting at a Far Meridian" book's author, it's not Holmes, but Wilson.
So the spinor or electron geophysical model, as Igor called it, presented in previous comments, is in fact just a combination of oscillation and rotation. Drawing it on paper maybe helps with clarity.
Make a circle r=1 and mark φ=+pi/3 or φ=-pi/3 position on it, the projection of such a radius vector on x-axis is 1/2 which represents projection of the spin "vector" to direction of momentum. This "unit" vector oscillates between these two positions, in total making 2pi/3 between them. It does not rotate strictly speaking, just oscillates or let's say reflects over the x-axis.
During the "exchange" of vector's positions, the whole circle rotates about y-axis with the same frequency, meaning that during half of circle rotation, vector switches from +pi/3 to -pi/3, or vice versa, at this point that's not so important. What we got is the rotating unit sphere with a radius vector oscillating in perpendicular direction to rotation. As a result, the vector's projection to x-axis also oscillates, between +1/2 and -1/2 for every half of the sphere's rotation, which when we "add" the rotation and oscillation together, makes for total angle change of 2pi between these two states.
Hopefully that makes it a bit clearer than before.
Taking things in still smaller steps, after oscillation for pi/2 the vector would be pointing in the direction of x-axis which got rotated for pi/2 about y-axis and now pointing in the direction of z-axis. So, for combined total change for the angle of pi, vector's projection to "outside" direction pointing in the x-axis direction of the circle at rest (direction of momentum for example), would now be 0. Similar would be for rotation and oscillation of 3pi/2, or for combined angle of 3pi.
If we now plot the projection as a function of combined total angle change, or look how things appear like in the plane of apparent vector's rotation, we get the total "period" of 4pi, that is two-valuedness of a spinor.
Was this explanation helpful?
P.S. Just to be clear, when said "vector oscillated for pi/2" for example, this is meant in terms of frequency, that is in terms of the circle's or sphere's rotation about y-axis, not in terms of the actual angle or the latitude on the sphere vector traveled. Oscillation for pi/2 then simply stands for a quarter of total complete oscillation represented by 2pi.
DeleteSo the "total combined angle change" would be 'measured' in sort of units of rotation and oscillation frequency. For example, changing the position from +pi/3 to -pi/3 is half of vector's oscillation which would enter in total combined angle as pi, and together with standard rotation for pi would give total 2pi.
Depending on the outside viewpoint, that is on chosen fixed orientation of axes of some outside reference system, we could we see this oscillation+rotation "system" as a oscillating line (projection on x-y plane) or a circle (viewed from the point on the meridian of oscillation perpendicular to the direction of oscillation) or an ellipse (projection on x-z or y-z plane).
DeleteThat fact tentatively suggests that gravitation and electromagnetism, as per Ark's "question" few weeks ago, are in fact a matter of observation.
If our observational line of sight coincides with the radial direction of the observed osc.+rot. spherical system, it might be said that sort of so called polar slope, that is the angular difference between tangent to sphere and our line of sight, would be 0, and sort of only information we would record about the observed system would be its size in terms of the solid angle perceived, that is area/r^2 when observed from a distance r. Similar would happen if the system kind of observed itself by reflection on its surroundings looking along the axis of its rotation.
So, to get an idea of its actual size, the system would need to find a spot at the distance from the mirror, as in the object on which it reflected its image, where its perceived reflected size would not change anymore. Then it could conclude that observed size, as in sort of area or solid angle, would correspond to opening of its perspective or let's say eye. In model presented in previous comments an eye would correspond to opening angle of the "oscillating" vector, which in this case would be sort of static and just rotating together with the sphere around the axis of rotation.
That would represent sort of gravitation in the sense of a distance where stable orbits for given orbiting rotating objects could be found. Polar slope close to 0 would translate into weak gravitation strength, in the jargon of modern "disjoint from nature" scientific parlance. At that point the oscillation of so called "observational vector" (representing directional reflection) might start to happen, which together with sphere's rotation could be related to magnetism and consequently to so called EM force as understood in nowadays physics.
In principle, a system could begin with only being aware or conscious of its existence in a sense of a difference from its immediate surroundings, and just by observation could inform itself about basically everything, gaining more weight as in knowledge and energy with each successive or iterative round of observation as in rotation coupled with reflection.
FWIW.
From the very beginning of this post, realized that i have an awful mess of subspaces, ideals, and operators...((
ReplyDeleteArk, could you explain once again why do we need two different types of operators "trace-class" and "Hilbert-Schmidt" and what is the subspace B1 here: B1(H)⊂B2(H)⊂B(H)?
One consolation is that it dawned on me why ideals are crucial elements of our consideration! Ideals are like boudaries - they have zero norm, i.e., zero size in the metrics of the host space: like 2d surface has zero 3d volume, etc.
Ideals capture the idea of the 'edge of world', the infinity, where one will never get (without adding an extra dimension).
OK. Thanks for asking. I will write a separate P.S. on this subject.
DeleteArk, i figured out one of my misunderstandings!
DeleteIt was here: "ρ is a (faithful) density matrix in the IDEAL of trace-class operators".
So, i thought that the trace-class operators have their own ideal, and was completely lost in those nested ideals...:)
Now i looked into Part 48 and see that the trace-class operators ρ and the Hilbert-Schmidt-class operators ρ½ are both the ideals of all bounded operators B(H). The latter class B2 is wider and includes the former B1, but this does not mean that B1 is the ideal of B2, right?
B1 is an ideal in B. What that means? That means that the product of any element of B1 by any element of B is again in B1.
DeleteB2 is a subset of B. It follows that also the product of any element of B1 by any element of B2 is again in B1. Thus, a fortiori, B1 is an ideal in B2.
Is it more clear now?
"B2 is a subset of B" --> "B2 is a subset of B1"
DeleteYes, thanks a lot. Now reading the new PS...
The first "Why?" is not hard
ReplyDelete"Notice that if H is infinite-dimensional, then lim_n p_n = 0 (Why?)"
Since ∑p_n = 1, we need a finite sum of infinite number of terms, therefore, starting from some n, they need to be all zeros.
Not quite. Look here:
Deletehttps://tutorial.math.lamar.edu/classes/calcii/convergenceofseries.aspx
and scroll down to Theorem.
"Access is forbidden"...:((
DeleteI will try other sources
Added screenshot from the site in P.S.
DeleteYes, i see, thank you! Right, rigorously speaking, the difference between two elements of the sequence should tend to zero when 'n' tends to infinity.
DeleteThis comment has been removed by the author.
ReplyDelete"Exercise 1. Prove that e_m,n∈B2(H)"
ReplyDeleteFirst attempt to do it:
We want to show that Tr ((e_mn)*e_mn)<∞, so we assess the trace:
Tr((e_mn)* e_mn) = Sum_i(e_i, (e_mn)* e_mn e_i) =
Sum_i(e_i, e_nm e_mn e_i) = Sum_i(e_i, |e_n)(e_m||e_m)(e_n| e_i) =
Sum_i(e_i, |e_n)(e_n| e_i) = Sum_i(e_i, |e_n)δ_ni = (e_n|e_n) = 1
A strange result...
So, they are unit vectors. Now you need to show that they are mutually orthogonal.
DeleteIn order to show that they are mutually orthogonal, we need to calculate the scalar product, i.e., the trace:
DeleteTr(e_mn* e_m'n') = Tr(e_nm e_m'n') =
Sum_i(e_i, |e_n)(e_m||e_m')(e_n'|e_i), which is nonzero only if m=m'. Then, for m=m' we have (e_m||e_m') = 1 and
Tr(...) = Sum_i(e_i, |e_n)(e_n'|e_i) = Sum_i(e_i, (e_n', e_i)e_n)=
Sum_i(e_i, δ_n'i e_n) = (e_n', e_n), which is nonzero only if n=n'.
Hence, for m≠m' and n≠n' the scalar product is zero and vectors e_mn and e_m'n' are orthogonal.
That is exactly what we needed. But there is a final touch needed: to show that it is a basis. For that we need to show that if A is an element of B2(H), and A is orthogonal to all e_mn, then necessarily A=0.
DeleteThis is already a path i have slightly used to.
DeleteWe take zero scalar product, express it as a trace and a sum:
0 = Tr(A, e_mn) = Sum_i (e_i, A e_mn e_i) =
Sum_i (e_i, A |e_m)(e_n| e_i) =
Sum_i (e_i, A (e_n, e_i) e_m) =
Sum_i (e_i, A δ_ni e_m) = (e_n, A e_m) = 0
for any m, n.
Then, should we repeat the considerations from Part 48?
Finite combinations of e_m and e_n span a dense set.
A is in B2(H), hence, it is a bounded operator and, therefore, is continuous. So if A vanishes on a dense set, it vanishes on any vector by continuity.
That is very good. Exactly what was needed. It only may look a little bit scary when you do it first time.
Delete:)) Thanks for support! It is still a long way for me to go: commutants and modular automorphisms are waiting to be clarified.
DeleteThis comment has been removed by the author.
ReplyDeleteSorry, i don't understand why the angle brackets eat all between them and how to fix this...
ReplyDeleteLook her:
ReplyDeletehttps://stackoverflow.com/questions/14659240/angle-bracket-without-triggering-html-code
I am using it ">" and "<".
"i think we can just write formally
ReplyDelete(JS , JT) = (S*, T*) = (T, S)* = cc(T, S)"
It is not only "formally". It is really true.
But is should be expanded using trace property:
ReplyDelete(JS , JT) = (S*, T*) =Tr(S**T*)=Tr(ST*) =cc(Tr((ST*)*))=cc(Tr(TS*))=cc(Tr(S*T))=cc((S,T))
This is however not needed if we assume that (S,T) = Tr(S*T) has indeed the scalar product properties.
ReplyDeleteYes, i wanted to use trace, then decided that it is not necessary but could not explain why. Ark, your comments make my blurry picture sharp.
ReplyDeleteNow about commutant. I looked for a definition and found this: https://en.wikipedia.org/wiki/Commutator_subgroup
But it seems to be not that you mean here...
Added a P.S. that may help?
ReplyDeleteYes, thank you, it is easier than i thought after reading Wikipedia; though i liked the idea of commutant as a measure of how far the group is from being abelian.
ReplyDelete< check of brackets >
In today's P.S., paragraph or line 5,
ReplyDelete"If a\in C^\prime then ac=ca. That is c\in C^\prime."
Is that correct, should the end statement, logical conclusion, perhaps be that c is in C'', that is c is C prime-prime like commutant of C'?
Thanks. You are right. I kind of corrected it, but it is hard to correct because on McCarthy's web site tex symbols are converted to images.
ReplyDelete"Therefore, Jπ(a)J = π'(a*), and the equality Jπ(A)J = π'(A) follows (Why?)"
ReplyDeleteI would say that it is because algebra A is a *-algebra with involution and every element 'a' has its conjugate pair a*. Thus, by taking one by one all elements 'a' of algebra A on the left-hand side and looking for the corresponding a* on the right-hand side, we obtain the algebra A of a*s, which is again A but "in another order". So the whole algebra A is translated into itself, and one can write 'A' instead of 'a' in the equality considered above.
Such an informal explanation, but i don't know how to formalize it.
@Saša March 19, 2025 at 5:02 PM
ReplyDeleteThank you for asking! I was staring for a long time at that C with one prime trying to understand how a subset can be its own commutant. Now all is in order.
@Ark, here are my belated attempts to grasp something else.
ReplyDelete"It follows then from the last statement in Fig. 1 that ρ^is is a unitary operator in B(H) (How?)"
Does the last statement at Fig.1 (x_f)* = x_f mean that operator x_f is unitary? The bar over f confuses me a little...
we have (How?)
The statement "Uρ(s) Uρ(s') = Uρ(s+s')" is simply addition of the exponent powers.
The statement "Uρ(s) Ωρ = Ωρ" is the consequence of (3):
Uρ(s)| a > = | ρ^is a ρ^-is > =| ρ^is ρ^1/2 ρ^-is > = |all factors commutate| => ρ^1/2