In our theory of EEQT we start with a fundamental and simple fact that material things (like chairs) exist, and that events happen (for instance a chair breaks). Any theory that does not have a place for these simple data will not be able to account for what happens. It will have to, for instance, imply that these things happen only in our minds, and then resign, because our minds do not belong to physics. That is what many of the so called “quantum philosophers” say. It’s a load of nonsense.
Quantum Fluctuations
One of the speculations made by theoretical physicists is that the “space-time metric fluctuates”. Time somehow becomes space, space somehow becomes time – in a way that is still speculative within the context of the orthodox quantum theory.
Alexsander K. Guts, a Russian physicist and mathematician from the State University of Omsk wrote an entire book entitled “Elements of the Theory of Time”1, where he discusses, in particular, possible scenarios of four and five-dimensional space vs. time fluctuations. According to him (and his collaborator, Marina S. Shapovalova2) the idea goes back to John Archibald Wheeler in 1960-1970, then followed by the famous Russian physicists, A. D. Sakharov, and an Italian iconoclast physicist G. Modanese. Modanese also became famous for his work on “antigravity”. According to the English Wikipedia:
Giovanni Modanese is a professor at the Free University of Bozen-Bolzano, Italy.
He is the author of several publications in General Relativity and Quantum Gravity. He collaborated with Eugene Podkletnov, devising a device that reportedly generates a "repulsive" gravity-like beam that is several orders of magnitude stronger than the aforementioned experiments. This work has been published in a peer-reviewed journal but has not yet been confirmed by others. (Italics, mine.)
Evidently there is something dangerous about these ideas; not all is revealed to the public, probably because the military are interested in this kind of work. But from my private correspondence with Modanese I know that he is quite serious.
Bu no one has yet addressed the fundamental problem of “what are quantum fluctuations?”
Many physicists are using this term – “quantum fluctuations” - in a misleading way, in a way that suggests that quantum theory can explain “fluctuations”, while instead of explaining it, a rather involved mathematical apparatus is being proposed that actually only serves to hide the real problem. Nothing can really “fluctuate” except in a theory that describes “quantum jumps”, and this is still a speculative idea, except, I would say, in EEQT, where it is described as a real process that can be simulated even on a personal computer.
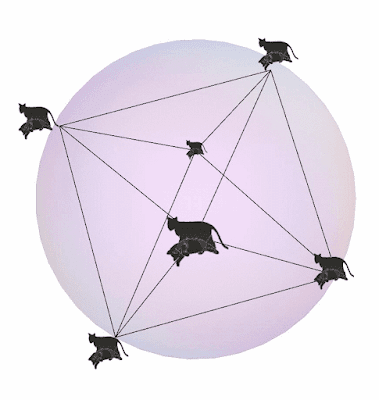
Here I will illustrate quantum fluctuations with a simple toy model that involves six Schrödinger’s cats that are continuously monitoring the simplest possible quantum system, so called “spin ½”. Quantum states of such a system (so called “pure states”) can be represented as points of the surface of an ordinary sphere. Each point on the sphere represents a direction of the spin (of an electron, for example). I have chosen six points on this sphere, points located at the vertices of two pyramids joined at their bases. These vertices form a regular octahedron – one of the five Platonic solids. At each vertex I put one of Schrödinger’s cat that monitors the direction of the spin, whether it points in his direction or not.
If the direction of the spin points in the direction of the cat – the cat dies. But, because I adore cats, my cats are immortal. Right after their deaths they get resurrected and start watching again. When a given cat dies, quantum state jumps – usually in the direction of the cat that got hit by the spin. Since the other cats are observing as well, we have a sequence of jumps. Each time when the quantum state jumps I note the new position of the direction of the spin state by a white point on a black sphere of quantum states. The jumps are random, according to a particular algorithm proposed by EEQT. And yet, after ten million random jumps, simulated on a PC, a strange (and not fully understood yet) fractal pattern appears.
Two things are “fluctuating” here. First there are cats that repeatedly get killed and resurrected, but I am not interested in their reincarnation histories here. I am interested in the fluctuating state of the quantum system – the pattern drawn on the invisible “quantum sphere”. The Russian physicist from Omsk, Guts, also has an idea of fractality that may be important for space and time fluctuations. In EEQT, in this example with six cats, one of the well known quantum dogmas is being questioned, since according to the textbook quantum theory my arrangement of cats is not allowed by Heisenberg’s uncertainty principle. But Heisenberg was not God, and a textbook should not be considered as a Holy Bible. To have some fun I published my paper in the Chinese Journal of Physics,
1Aleksandr Guc), “Elementy teorii vremeni”, Art&fakt jelektronnyj al'manah Omsk: Nasledie. Dialog-Sibir', 2004 (in Russian)
2Alexander K. Guts, Marina S. Shapovalova, “Large fluctuations of time and change of space-time signature”.
P.S.1. The fractal above reminds me of Bach's Toccata and Fugue. My wife loves this particular perfect performance, so this is for her.
P.S.2. 22:24 Why SO(4,2)? One important, attached to Reality, reason is here: M. Wnuk, "The electromagnetic nature of life--the contribution of W. Sedlak to the understanding of the essence of life"





"In our theory of EEQT we start with a fundamental and simple fact that material things (like chairs) exist, and that events happen (for instance a chair breaks). Any theory that does not have a place for these simple data will not be able to account for what happens. It will have to, for instance, imply that these things happen only in our minds, and then resign, because our minds do not belong to physics.".
ReplyDeleteOk. I can agree with you on this point, that material objects such as chairs, tables or plush unicorns do exist. However, thoughts also exist. Numbers also exist. Photons and electrons also exist. Emotions exist. And they all exist in other ways. However, objects from the world of ideas show a picture of superposition, while classical objects are like after a collapse.
Physics induces laws from phenomena, Hegel sought a way of explicitly deducing phenomena from the Absolute. I wonder which approach is more appropriate, but I always lean towards the fact that the higher the abstraction the closer to the truth.
How does EEQT distinguish between the mode of existence of an electron and the mode of existence of a chair? I know this question may seem naive, but I am no longer afraid of asking such questions.
"How does EEQT distinguish between the mode of existence of an electron and the mode of existence of a chair?"
DeleteThis is a relevant question and it will be addressed in due time.
From your pdf file:
ReplyDelete"Evidently, for a given a, the points x for which 1 + 1a · x + a · a = 0 are
transformed into points in the conformal infinity.".
So, after applying the conformal transformation, you will move all points satisfying this equation to conformal infinity.
And what is the physical interpretation of this? What do these points represent?
1 + 2a · x + a · a = 0. Corrected.
DeleteI don't know. Yet.
"1 + 2a · x + a · a = 0. Corrected.
DeleteI don't know. Yet.".
And I am thinking that the conformal infinity, to which points satisfying a given equation are transformed, can be interpreted as a kind of 'event horizon' for the observer. In the context of cosmology, for example, conformal infinity can be interpreted as the limit of the observable Universe.
If the points that satisfy a given equation are transferred to conformal infinity, this means that the observer is not able to receive information from these points after the transformation. This can be compared to the situation where the observer is in the vicinity of a black hole: the observer is unable to receive information from points beyond the event horizon of the black hole.
One can define a forgetting functor, since O(4,2) is a smooth manifold and this procedure would not be nonsensical. So we can lose information about the category structure. This is interesting, although I have another question. Does the O(4,2) group capture all substructures of the physical temporal structure?
Or put another way: how could O(4,2) solve the black hole information paradox? For I would now define an equivalence relation... After all, information cannot be lost and this must be taken into account. Hence equivalence relations and quotient categories. In the structure of metacategories, information is encoded. In some small categories it is lost. In this view, information should be modelled as a curvature of quantum state space analogous to gravity at larger scales.
Similar questions are being addressed in this paper
DeleteMashhoon - Conformal Symmetry, Accelerated Observers, and Nonlocality, Symmetry-11-00978
https://www.mdpi.com/2073-8994/11/8/978
It seems via previous posts like there's three separate uses for O(4,2), bosons (gravitons) aka algebra not center for EEQT; a differential geometry G-structure for gravity aka EEQT algebra center; and conformal infinity aka twistor spacetime basis vector structure where the conformal infinity is an interface of sorts between the 4-dim universe and the 4-dim anti-verse. An SU(4,4) could be an 8-dim G-structure.
Delete@Ark
ReplyDeleteWill you be publishing this paper on conformal groups or parts of it or putting it on archive? I would like to quote several elements from this paper in my work.
It's just an embryo. To early to tell the future of it.
DeleteSomething worth looking at:
ReplyDeleteR. Fioresi; E. Latini
The symplectic origin of conformal and Minkowski superspaces
J. Math. Phys. 57, 022307 (2016)
https://arxiv.org/pdf/1506.09086.pdf
"... In geometry, in fact, ”objects” are built out of local pieces:
the most general of such object is a superspace, and the symmetries of such an object are then supersymmetries which are described by supergroups.
The functor of points originally introduced by Grothendieck to study algebraic geometry, is now an essential tool to recover the geometric nature of supergroups and superspaces, which is otherwise difficult to grasp through the sheaf theoretic approach."
Bjab -> Ark
ReplyDeleteW wielu miejscach tildeM
W wielu miejscach tildeu
W (13) y w wykładniku
Pod (14) jest immediately follows. Wiemy co prawda co nieco o x4, y4 i x6, y6 ale nie wiemy o zależnościach dla 1 2 3 5.
Thank you very much. Will fix it in the new version.
DeleteThough the last sentence is not clear to me. To which part of the file it is addressed?
DeleteChodzi o zdanie pod wzorem (14).
DeleteUdowodniłeś, że (x4,x6) = +- (y4,y6) ale z tego chyba jeszcze nie wynika, że pozostałe cztery współrzędne są takie, że X = +-X'
"Though the last sentence is not clear to me. To which part of the file it is addressed?"
DeleteThis is about this:
"From u(X) = u(X0) it then immediately follows that X = ±X0, therefore [X] = [X0].".
After formula (14), page 3.
Bjab -> Ark
DeleteJednak raczej wynika.
Good. Indeed, it follows when looking at (4). Other typos corrected. Thank you!
DeleteW temacie punktu 3-dgo występuje jeszcze tildeM.
DeleteWe now define The ->
We now define the
embedding ̃τM → τM ̃ ->
?
wzór (17) ->
?
Now, if XN ->
?
and X5 /= X6 ->
dlaczego wielkie X a nie małe x?
i dalej znowu tildeM w dwóch miejscach
Thanks. These are the results of "Replace All" command. Now will have to check and fix All.
DeleteFixed. Continuing with the unfortunate section 7.
DeleteBjab -> Ark
DeleteNad wzorem (17) jest:
"We now define The embedding"
Dlaczego The piszesz wielką literą?
Pod wzorem (17) jest:
Now, if XN
Chyba brakuje znaku należenia. (Trzy linijki niżej też brakuje).
Bjab -> Ark:
Delete"It follows that the points of M ̃ which are not in the image of
M ̃... "
tildetau?